In this post, we will review the paper Geometry Consistent Generative Adversarial Networks for One Sided Unsupervised Domain Mapping from Huan Fu, Mingming Gong et al. published in CVPR 2019.
After defining the problem we want to solve and explaining the related concepts, we will go over the state of the art methods. After that, we will explain the proposed method and experiment results, and finish with the conclusion.
All images that are used in this post are taken from the reviewed paper or from its poster.
A presentation for this paper can be found here
Introduction
Notation
Before starting, we should briefly explain the notation we will use in the rest of this post for completeness.
Script letters such as denote domains. Uppercase letters such as are used to denote random variables from the respective domains. Lowercase letters such as refer to samples from the respective random variables.
Domain Mapping
The goal of domain mapping is that given two domains and to define a mapping function between the domains. Using this mapping function, we expect to transform samples from domain to domain .
In our context, we will focus on images, so we are only concerned with mappings between image domains. This problem is also called image to image translation in the literature.
As an example, consider aerial images and maps. We know that for each aerial image there is a corresponding map or that such a map can be drawn. So, with a mapping function between the domains of aerial images and maps, we want to get maps for given aerial images.
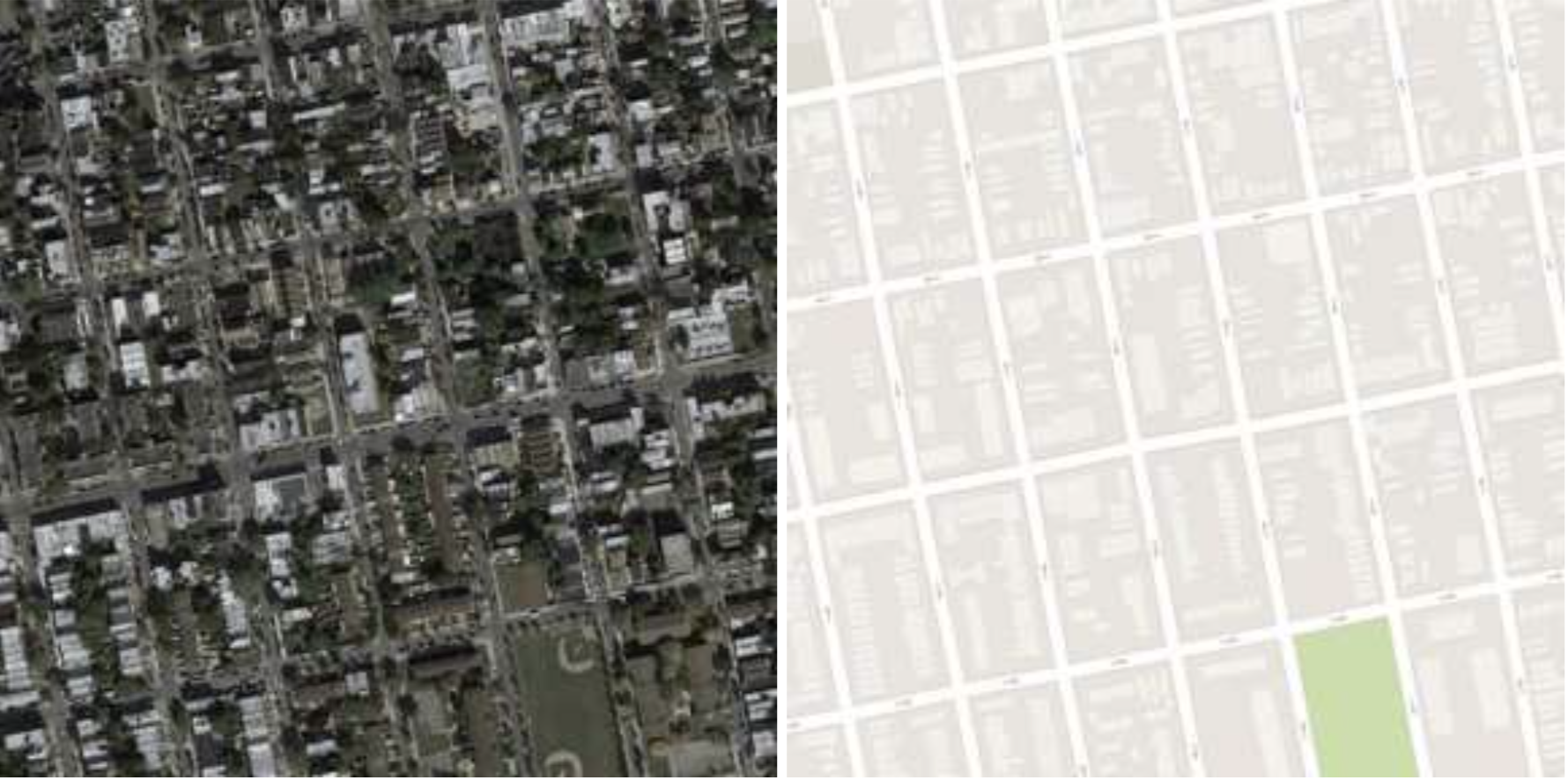
Unsupervised Domain Mapping
The problem of domain mapping can be studied with paired or unpaired data, i.e. in supervised or unsupervised manner.
As in other machine learning problems, studying domain mapping in a supervised manner is an easier problem with more related research.
Although supervised approaches can give very good results, the problem about it stems from the data collection step. To be able to apply supervised methods, we need paired images for our specific task. There are two problems about it. First, data preparation can be very hard or expensive for many applications. Second, it may not be possible to have corresponding images between domains at all. For instance, if we want to get paintings in the artistic style of Van Gogh for given photographs, we cannot provide paired data for supervised training of this task.
So, we focus on unsupervised domain mapping. For this, we don’t need to have paired data, it is sufficient to provide enough data for both domains. For instance, if we want to get zebra images from horse images, there is no need to provide paired horse and zebra images, it is enough to have images for horses and for zebras separately.
Unsupervised approach makes this problem more practical for real world applications, but the problem becomes more challenging as well.
The main challenge about unsupervised approach is that finding an optimal mapping function without paired data is an ill posed problem. It is an ill posed problem because we fail to ensure that any solution we find is uniquely optimal. In other words, there can be many mapping functions between two given domains and we cannot say that one is better than another. Generally what we need in order to solve ill posedness is to introduce new constraints or make new assumptions.
In a mathematical point of view, the goal is to model joint distribution using samples from marginal distributions and . Without any constraint, it is possible to infer these marginal distributions from infinitely many joint distributions. Thus, we cannot know if inputs and outputs are mapped in a meaningful way.
For supervised methods, the constraint is implicitly provided by the image pairs. So cross domain pairs are used to find uniquely optimal solutions. Sadly, we cannot use this constraint, so new constraints are needed to be proposed.
For unsupervised domain mapping methods, the proposed constraints are very important. It has a big effect on the learned mapping function, and also applying the constraint can require additional steps or changes in the proposed method.
In the next section, we will see examples of proposed constraints for image to image translation problem but before that there is another important concept we need to introduce.
Generative Adversarial Networks
Generative adversarial networks, or GANs in short, are very popular for domain mapping problem. Deep convolutional GANs especially are used for tasks such as image inpainting and style transfer.
The main idea of GANs is as follows. Two networks, namely a generator and a discriminator, are trained in a zero-sum game setup. Generator tries to generate indistinguishably realistic images while discriminator tries to distinguish real images and fake images generated by the generator. In this way, generator and discriminator simultaneously optimize each other.
Generating very realistic outputs is one of the main reasons of popularity of GANs for such tasks.
This main idea, namely adversarial constraint, can be summarized in a loss function as follows:
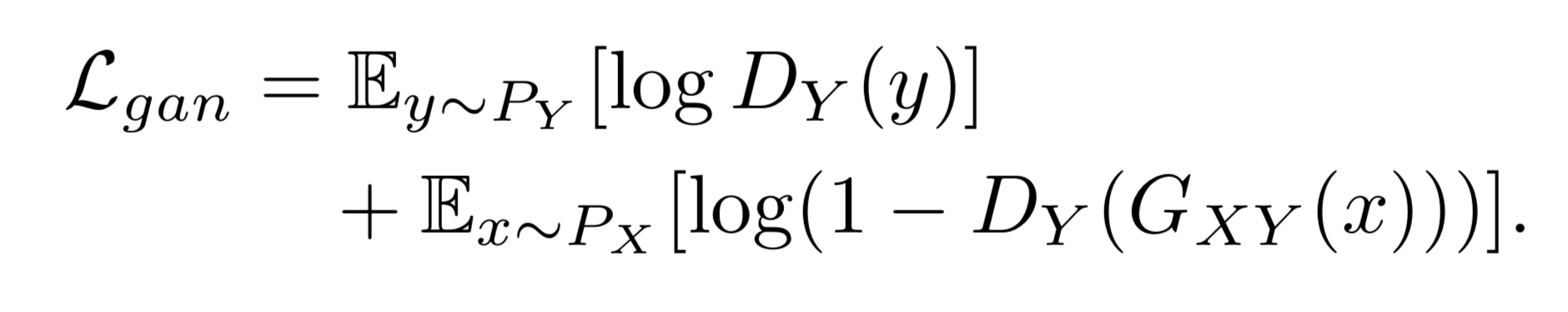
Above, denotes the generator and denotes the discriminator.
State of the Art
CycleGAN
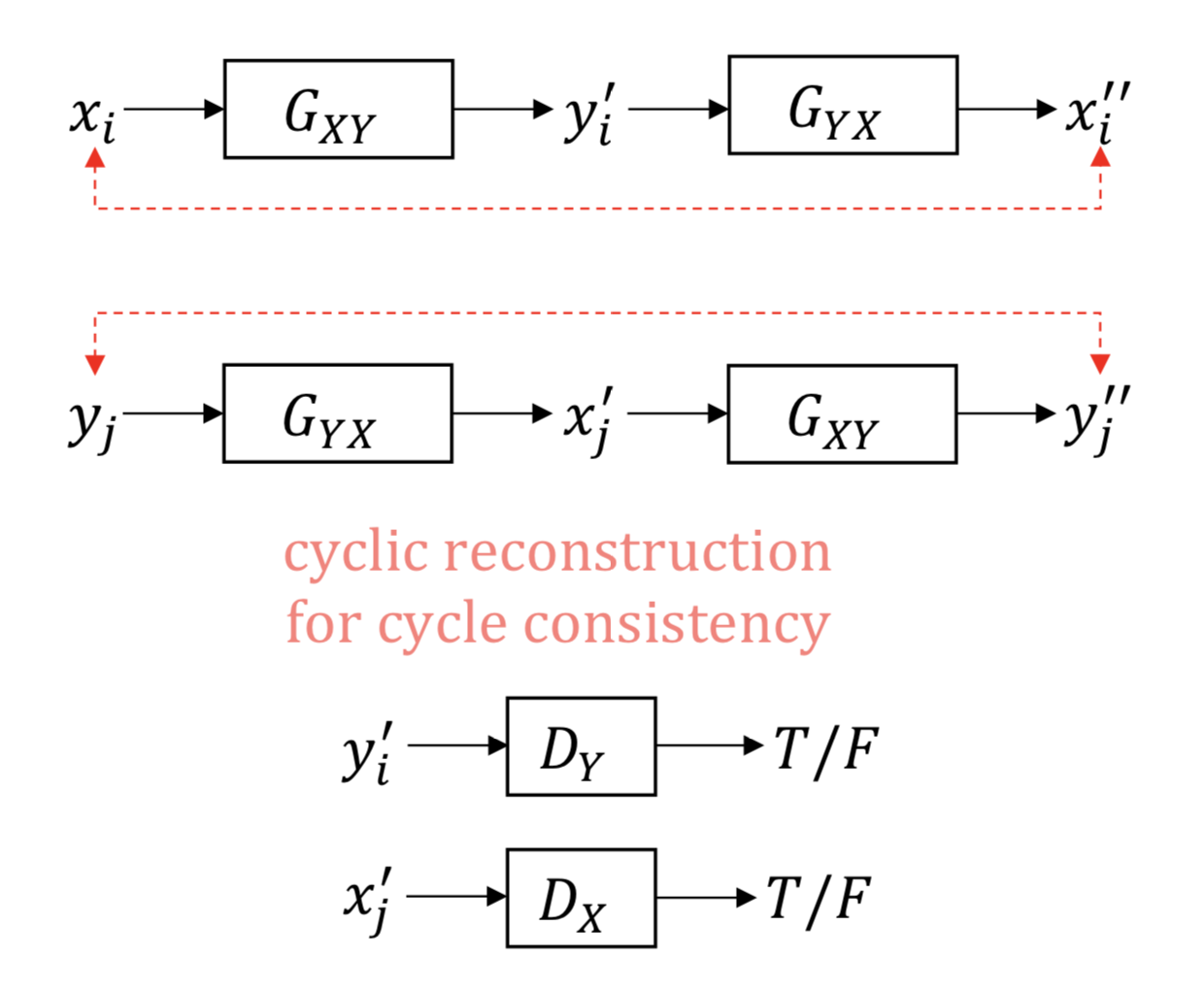
One popular assumption for unsupervised domain mapping is cycle consistency. The idea is simple but effective. If we map an image to the other domain and then map the result back to the initial domain, what we get should be very similar to the original image, ideally the same image. In other words, two mapping functions and its inverse should be bijections so composition of these functions should be identity function ideally or at least close to it.
We can write the related loss function for cycle consistency assumption as follows:
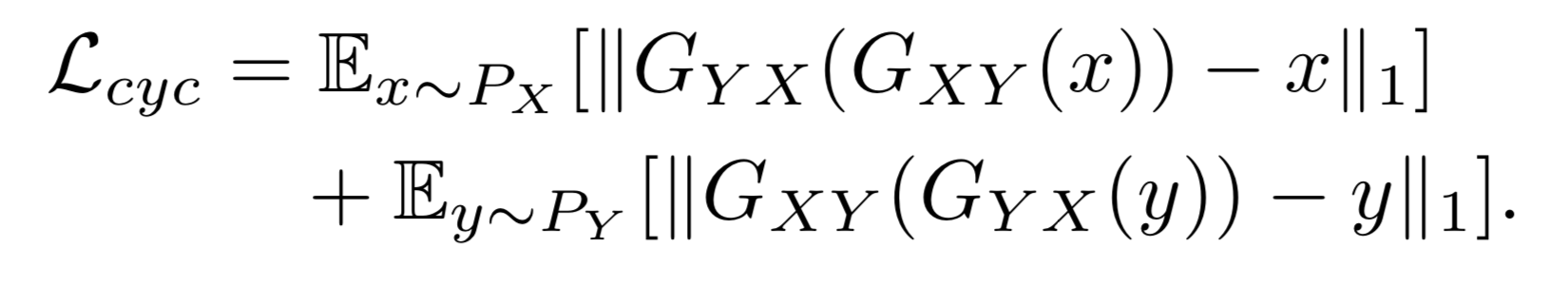
Cycle consistency assumption is very popular and after its initial proposal by CycleGAN (Zhu et al. 2017), DiscoGAN (Kim et al. 2017), DualGAN (Yi et al. 2017), there have been many proposals to improve it.
Here, one important property of CycleGAN and similar methods is that these are two sided methods, i.e. mapping functions and need to be learned jointly.
DistanceGAN
Another assumption for unsupervised domain mapping is that the distance between two samples in one domain should be preserved after they are mapped to the other domain. This is first proposed by Benaim et al. 2017.
For this, first we need to define how we measure the distance in given domains.
For a predefined distance function , we can write the following loss function:
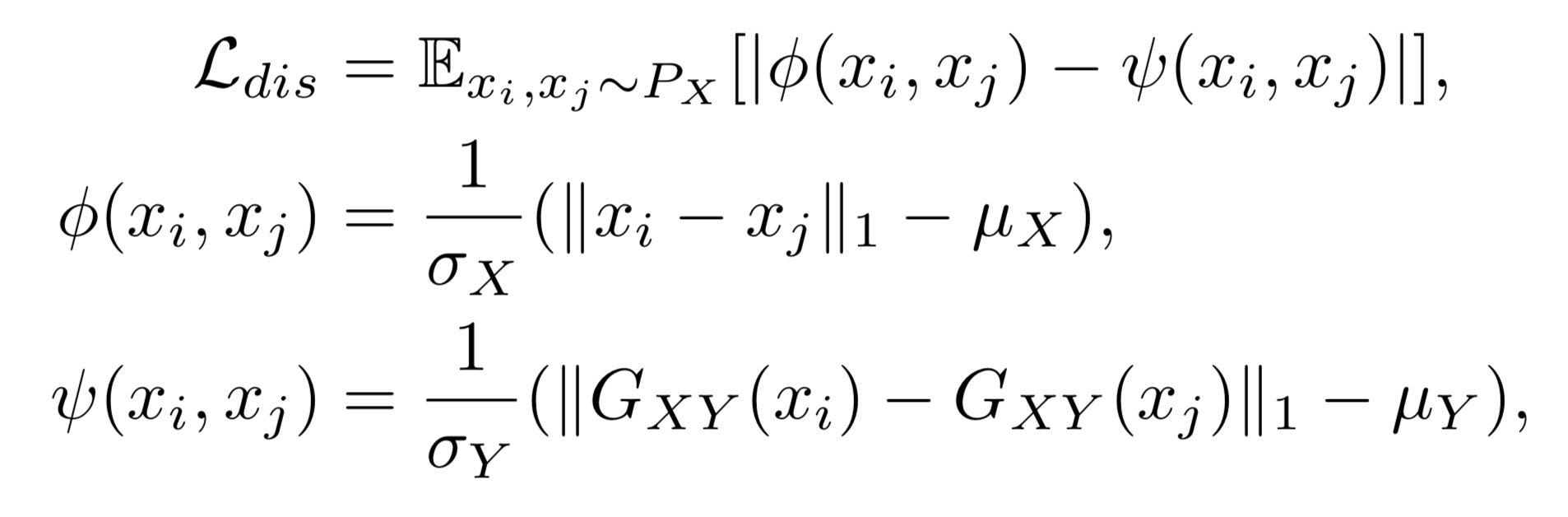
Here, distances are measured between samples and and also between their corresponding images in domain . These distances are first normalized in respective domains using distances of all possible pairs in those domains. After that, what is done is simply penalizing differences between two normalized distance measurements in domain and domain . Here, , are means and , are standard deviations of distances of all possible pairs in the respective domain.
Contrary to cycle consistency assumption, distance assumption is one sided, i.e. can be learned without learning .
Proposed Method
Intuition
The main idea behind the proposed method is that simple geometric transformations preserves semantic structure of the image.
Here, what is mentioned with simple geometric transformations are transformations without shape deformation. This can be thought of as any movement you can do using a camera without touching the recorded object, e.g. rotation or translation in 3D space. Since we work on already taken images, we cannot change the perspective much. We can rotate the image which corresponds to rotating the camera in z axis. So, possible transformations we can apply are limited.
Semantic structure in this context means any information that distinguishes object classes, that humans are already able to see.
So, if we keep using aerial images – maps example, seeing the aerial image or map in different orientations does not make any difference, as humans we can still say that they are aerial images or maps and we can still relate between matching samples.
Geometric Transformations
In this paper, only two transformations are used as a proof of concept. These are 90° clockwise rotation, denoted as rot, and vertical flipping, denoted as vf. Rotation is more dominantly used and it is the default transformation for the proposed method.
Geometry Consistency Constraint
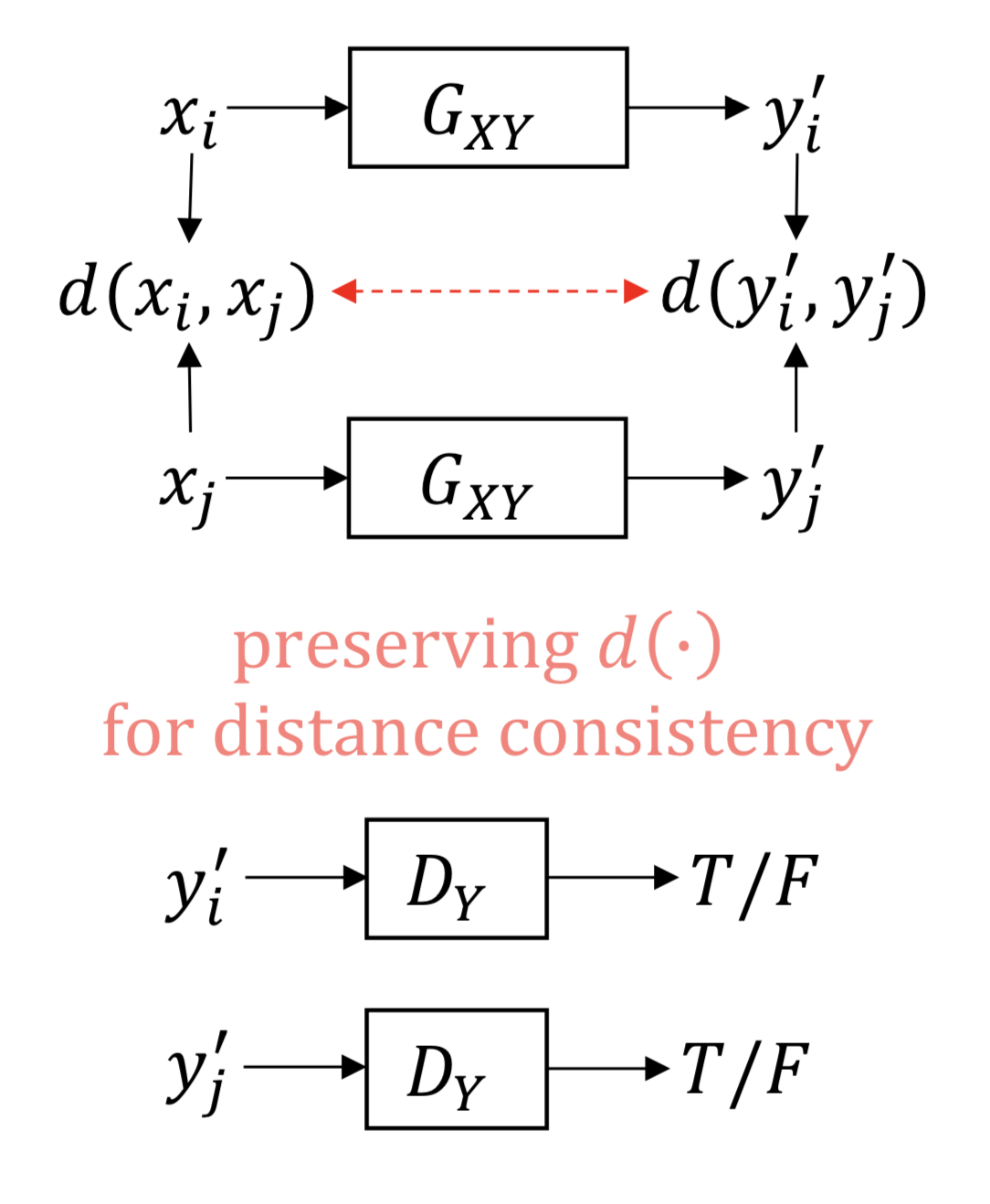
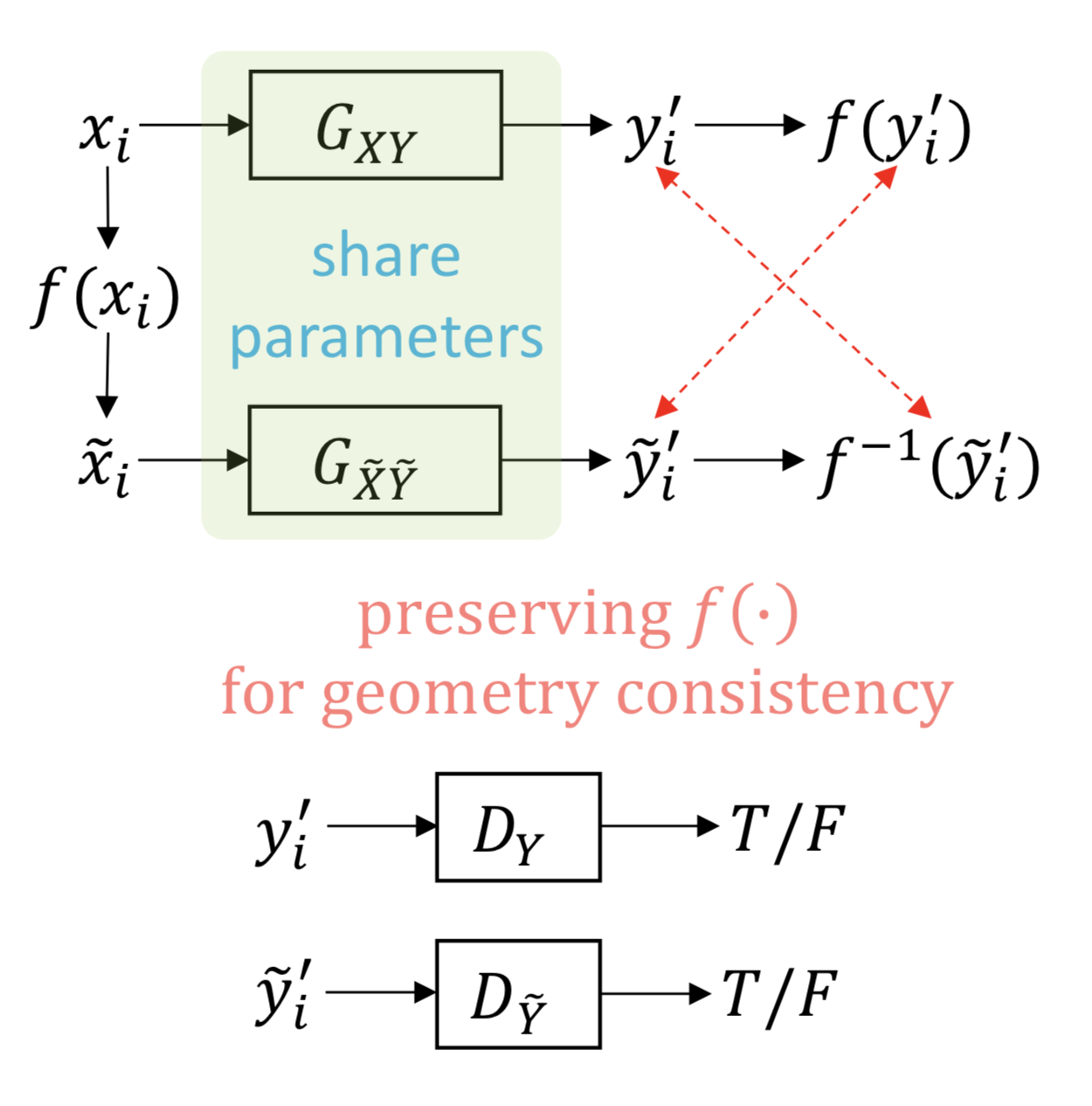
With this reasoning, the following assumption is proposed. For a geometric transformation function , where we get domains and by applying to domains and respectively, geometric transformation between input images should be preserved by mapping function and .
In other words, if we apply a transformation to an input image, the output should also reflect this geometric transformation. First translating from domain to domain and then applying should give the same result as first applying and then translating from domain to domain . The order we apply transformation and corresponding mapping function should not affect the output.
We can write this geometry consistency constraint as follows:
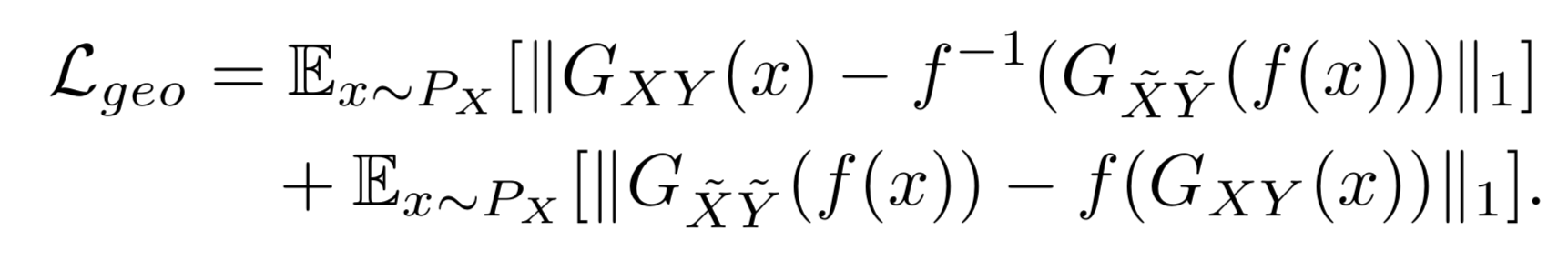
Here, one possible interpretation is that we should be able to reconstruct the mapping of an input image by first transforming it to domain before mapping to and then transforming it back to using inverse function .
In combination with geometry consistency constraint, the proposed method, namely geometry consistent GAN, or GcGAN in short, also employs adversarial constraint explained above. So, the resulting objective function becomes:
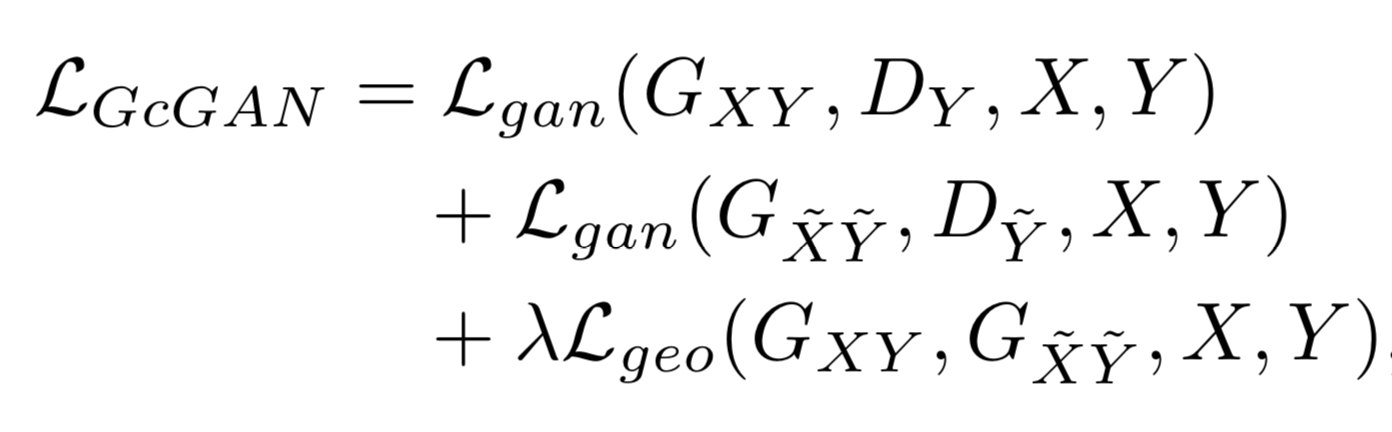
Here, is used as a hyperparameter which might require fine tuning for specific tasks.
Although there are two mapping functions and , they have the same architecture and share all their parameters, so they are actually one single translator. By training a single translator, and co-regularize each other as we don’t expect both mappings to fail at same regions of the image, failed mapping will be corrected by the correct mapping. This way, geometry consistency will be ensured locally.
Let’s give an example of GcGAN using aerial images and maps, and compare the results with the baseline model of this paper, namely only GAN without any additional constraint:
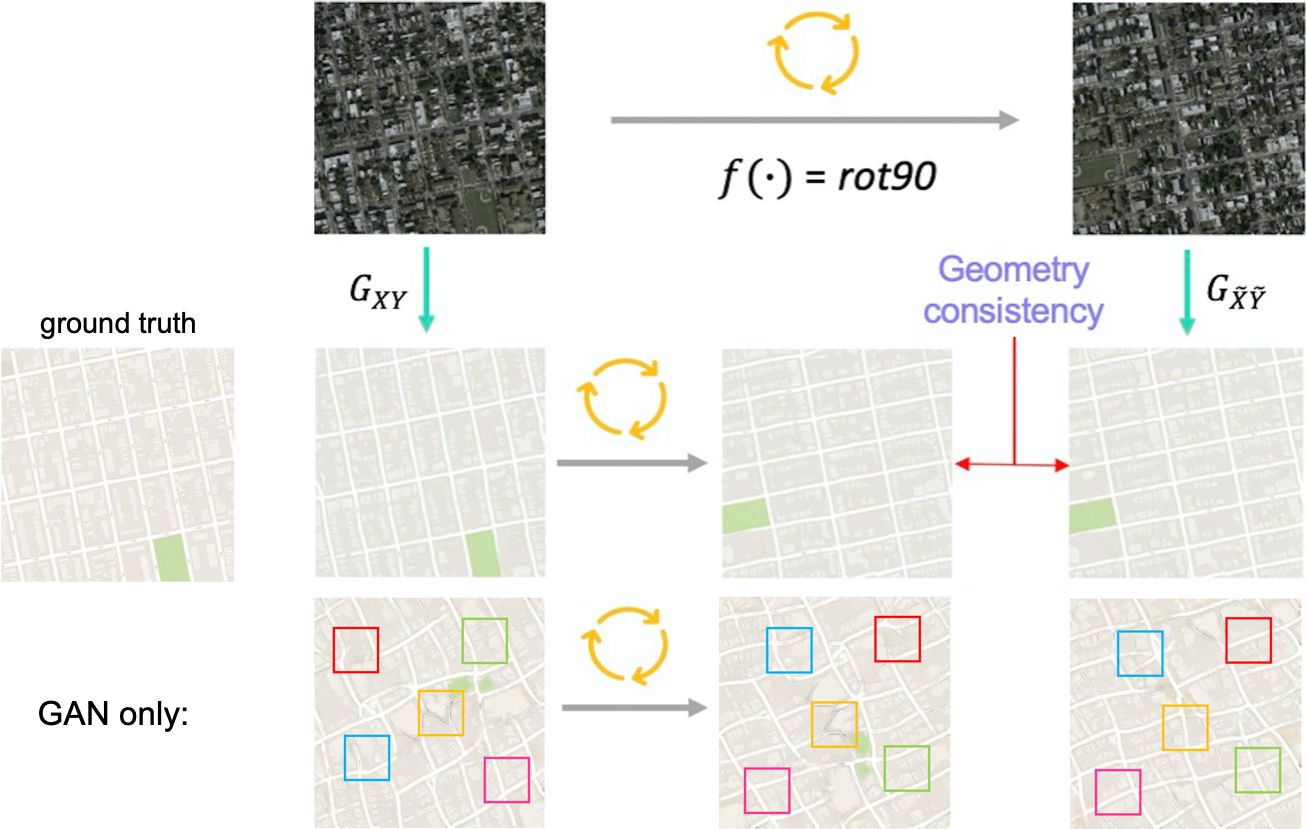
As it can be seen in the framed sections on the output of baseline model, there is no geometry consistency between outputs of original and rotated inputs. Although there are locally better parts in both outputs, the baseline model does not benefit from that while it is used by GcGAN via co-regularization feature. When we add geometry consistency constraint, it can be observed that there has been an important improvement in outputs both for geometry consistency and accuracy.
Similar to DistanceGAN, GcGAN is also one sided as we only train one translator.
Network Architecture
This paper does not propose anything regarding the network architecture and the same architecture from CycleGAN paper is used. As the main focus of the paper is completely on the proposed constraint and its comparison with the state of the art constraints, we also don’t want to focus on the network architecture. Generator is a standard encoder - decoder where encoder contains convolutional and residual block layers and decoder contains deconvolutional layers. Details of the architecture can be seen in Table 4 in arxiv version of the paper.
Experiments
Cityscapes
The main experiment setup is based on Cityscapes dataset. It provides images and corresponding semantic segmentations. For segmentation, there are 19 category labels and one ignored label.

In the dataset, there are 3975 image – segmentation pairs where 2975 pairs are used for training and 500 pairs (originally for validation) are used for testing. Testing pairs from the dataset are not used. Also pairing information is not used during training.
For this dataset, there are two tasks: generating segmentations using images and generating images using segmentations.
From images to segmentation
For this task, generated label colors are converted to class level labels using nearest neighbor search.
From segmentation to images
For this task, to evaluate generated images a predefined model for predicting semantic segmentation is used. Since we expect the generated images very close to the real images, segmentation of these generated images should be very close to original segmentation as well. So, after generating images their segmentations are predicted.
Evaluation Metrics
Predicted segmentations and ground truths are compared using pixel accuracy, class accuracy and mean IoU which are common metrics for semantic segmentation evaluation.
Pixel accuracy just measures the percent of correctly labeled pixels. This metric does not work well if the data is unbalanced, e.g. if half of an image is labeled as sky out of 20 different label classes.
Class accuracy measures pixel accuracy per class and takes the average over the classes. A similar problem occurs for class accuracy as well. If there is a class with large proportion, e.g. background class, never predicting that class would improve the overall accuracy.
The de facto metric for segmentation is mean intersection over union, IoU in short. It measures the area of correctly labeled pixels over the area of entire image per class, thus prevents the problem occurring with class accuracy.
Results

Looking at the qualitative results, we see that baseline GAN model does not perform well and for both tasks there are repetitive patterns which should not be there. For segmentation generation, CycleGAN produces sharper boundaries than GcGAN but it fails to correctly label the sky. GcGAN, on the other hand, produces a similar segmentation where sky is correctly labeled. This difference can be observed in other examples given in the paper as well but it is possible that while these specific samples produce this difference the difference cannot be observed in general.
For image generation from segmentations, we cannot expect very good results as it is a harder problem and results may be very different than the ground truth even when they reflect the segmentation successfully. In this particular case, both CycleGAN and GcGAN produced similar images while CycleGAN was not very successful about details of automobiles.
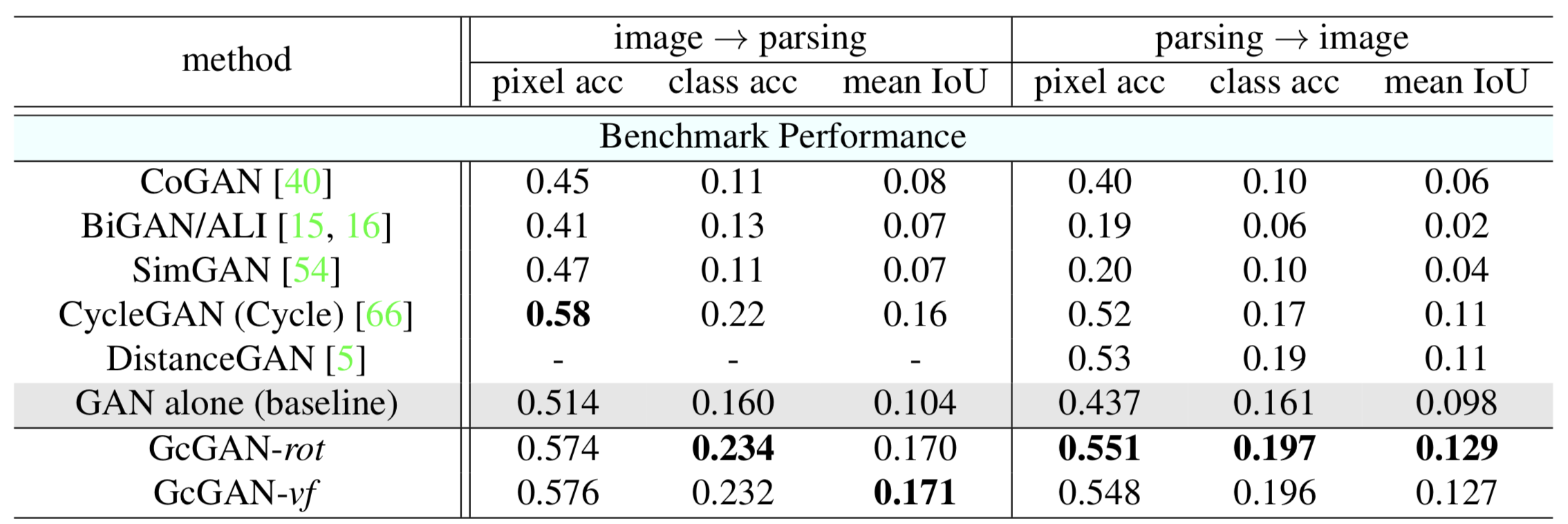
Both GcGAN with rotation and GcGAN with vertical flipping is evaluated. They performed similarly for these tasks although rotation works a bit better for generating images from segmentation.
The baseline method for experiments are GAN without any constraint. Methods other than the two state of the art methods perform worse than the baseline GAN model.
GcGAN performs better than the baseline for both tasks. For first task, GcGAN performs similarly compared to CycleGAN (0.6% better on average, 1% for mean IoU). For the second task, GcGAN provides 1.8% improvement over DistanceGAN.
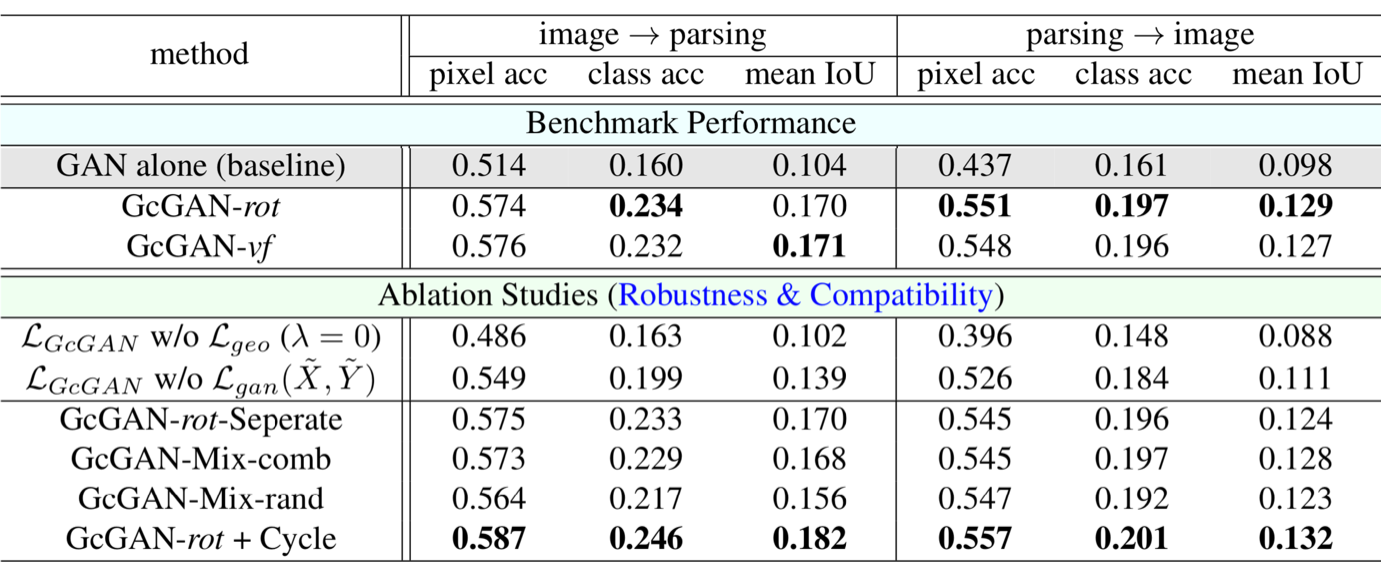
In this part of Cityscapes experiment, ablation studies are performed.
First, GcGAN is trained without geometry consistency constraint and without adversarial constraint. Without geometry consistency constraint, it performed worse than the baseline GAN model. One possible reason of this is the increased diversity of domains with addition of geometrically transformed samples. Interestingly, without adversarial constraint, it can still perform better than the baseline method. This confirms the effect of co-regularization of two mapping functions.
For GcGAN-rot-Separate, two generators are separately trained but did not provide any improvement. This shows that learning one generator for two mapping functions is sufficient.
Mixing multiple geometric transformations, either training with both transformations or selecting it randomly, does not increase the performance. The model can learn one transformation well but cannot learn multiple transformations efficiently.
The most important results from this part is that geometry consistency constraint can be combined with cycle consistency constraint. When two constraints are combined, it gives the best result in all metrics for both tasks.
House Numbers to Handwritten Digits

The task for this experiment is to generate handwritten digits from street view house numbers.
In this experiment, two datasets are used as two domains. SVHN is a dataset of house numbers collected using Google Street View images containing 73257 training and 26032 test images. MNIST is a handwritten digits dataset containing 60000 training and 10000 test images.
The experiment setup follows from DistanceGAN paper.
After generating output images, a pretrained model is used for classification of images.
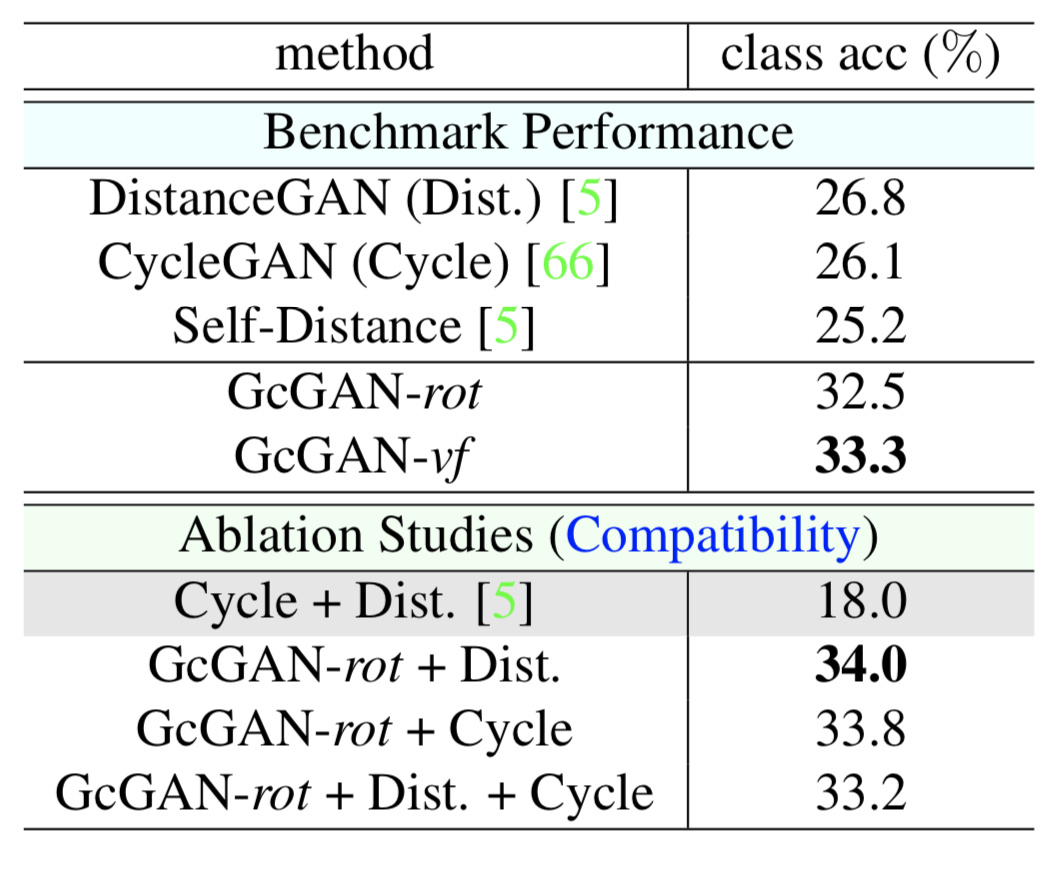
Here, GcGAN outperforms both CycleGAN and DistanceGAN. Although both GcGAN variants perform similarly, vertical flipping works better for this task.
Combining geometry consistency with other constraints improves the performance.
Aerial Images - Maps
For this experiment, 2194 pairs of aerial images and maps, 1096 for training, 1098 for testing, are collected using Google Maps around New York. Pairing informations are not used for training.

Both CycleGAN and GcGAN produces very realistic images from given map, while baseline GAN model is incorrectly visualize water body as green area. For map generation from images, CycleGAN is unable to classify all green regions correctly. Although the results are good, both CycleGAN and GcGAN had problems about correctly displaying some visual details on the map such as the small road in the park which is harder to see in the image.
There are quantitative results for only map generation from photos task.
As metrics, root mean square error (RMSE) and pixel accuracy are used. Since there are few number of colors in a map, for pixel accuracy, predicted and ground truth colors are compared by checking the maximum difference between RGB values, i.e. .
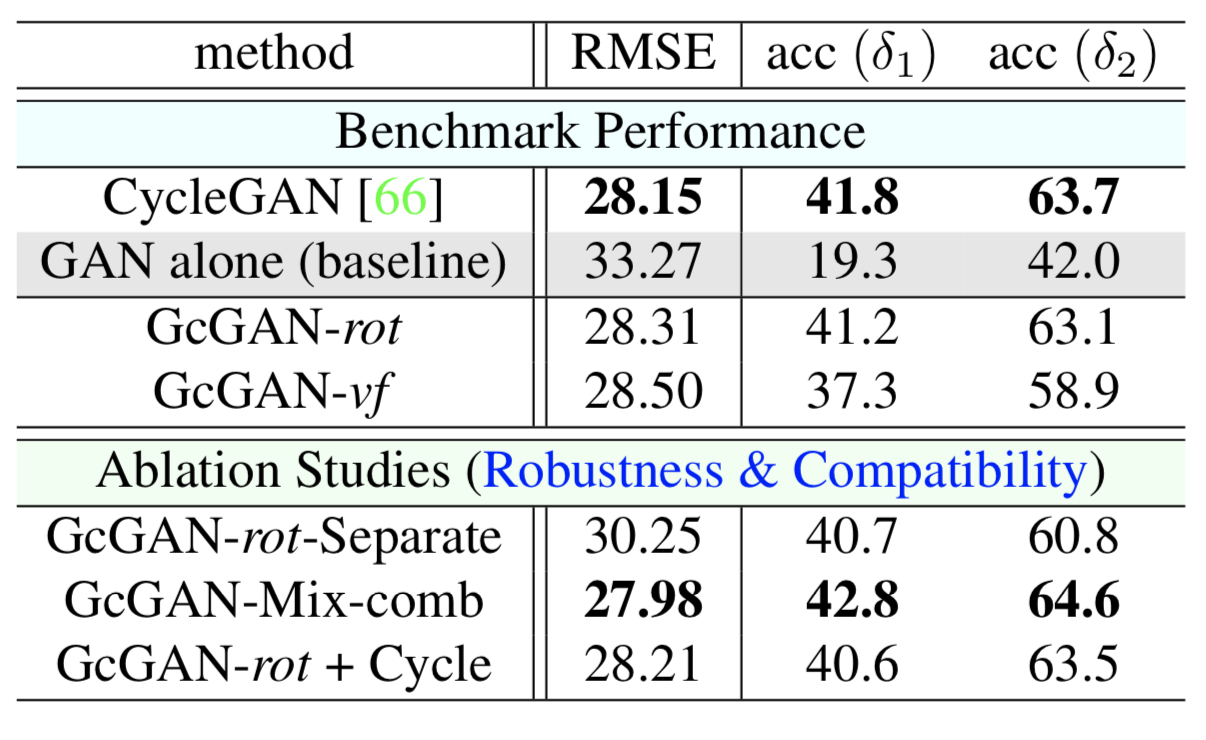
In this experiment, GcGAN achieves competitive results compared to CycleGAN yet CycleGAN is slightly better. For this task, using two geometric transformation functions for GcGAN, GcGAN-Mix-comb, gives the best results. This again indicates that, one may need to choose appropriate transformation or transformations and other configurations according to the specific task.
Qualitative Results
As image to image translation is a visual task, proposed methods are usually supported by many qualitative results. GcGAN paper also provides examples for various tasks. We will show some samples from these examples. For some examples, there is no comparison with other methods.
Although these examples are not enough to compare performance of different methods, for some cases GcGAN produces visually more impressive results compared to CycleGAN.

The result of GcGAN for photograph generation from Monet painting is very impressive.

For summer image generation from winter images, CycleGAN seems to be unsuccessful about removing the snow.


Conclusion
In the field of unsupervised domain mapping where cycle consistency constraint is largely used, authors suggest a new constraint which performs competitively or slightly better compared to state of the art constraints.
Ability to combine this new constraint with other constraint is one of the most important results. Although best performing combination depends on the specific task, using constraints in combination tends to perform better than default GcGAN and the best performing method. So, geometry consistency may not outperform other constraints individually but it improves state of the art when used in combination with other constraints.
The suggested assumption is very intuitive I think. Other than the newly suggested loss function, only requirement is defining a suiting geometric transformation function. They don’t suggest any change for the underlying GAN architecture and directly use the architecture from CycleGAN paper. This helps that the only focus of this paper is the proposed loss function and its comparison with other loss functions. They only study this particular part of the problem, making the interpretation of results easier and leaving room for studies about other aspects such as the network architecture.
In this paper, they only used two transformations as basic examples. Depending on the task, there might be more suitable transformations than rotation or vertical flipping. Also, not one of these transformations always performed better than the other. For Cityscapes experiment rotation works better while vertical flipping is more suitable for generating handwritten digits from street view house numbers. This prevents geometry consistency constraint to be as generic as cycle consistency constraint. Further study is needed about suitable geometric transformations for geometry consistency and their generality.
One possible criticism might be the use of CycleGAN from 2017 while it is mentioned in the paper that there are many publications about the improvement of cycle consistency. Assuming that these works improve the performance, they should take the best performing variation as the state of the art cycle consistency method rather than the first suggested version. The reasoning behind this choice might be the idea of comparing loss functions without touching other parts as we mentioned above. For this, they might have compared the suggested loss function with the original cycle consistency method. Still, there could be more recent methods in evaluations. We also should note that although this paper is from CVPR 2019 it is submitted to arxiv.org in September 2018 and last revised in November 2018.